Lattice models of quantum and statistical physics
An important feature of non-quantum finite-dimensional lattice models is principal ability to get numerically exact solution on a set of finite-size lattices suitable for doing finite size scaling and thus get approximate solution of any infinite model.
Mathematical tools
Lattice models of quantum chemistry
- Lecture on Second quantization in quantum chemistry 2021 [pdf]
- Lecture on Fundamental models of quantum chemistry 2021 [pdf]
- Lecture notes and code for symbolic solution of finite models are under refinement
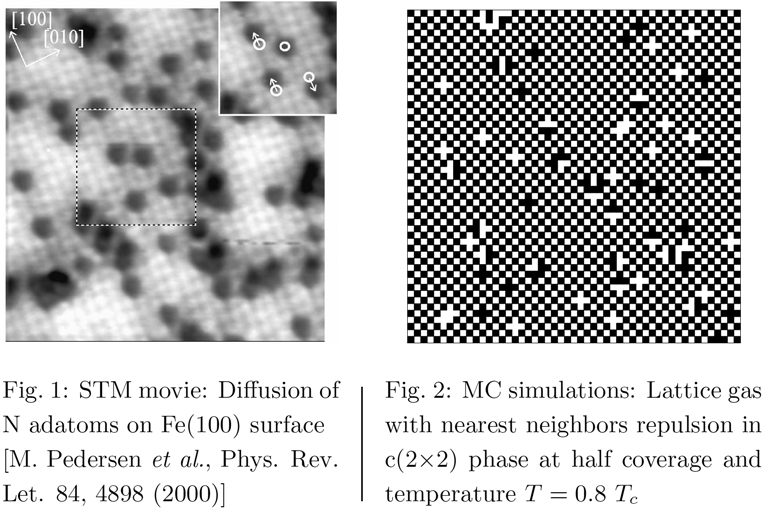
Lattice gas and Ising model: Dynamic correlation function of Ising antiferromagnet
Many dynamic properties of a lattice system is encoded in its equilibrium two-point two-time correlation function. Its calculation is nontrivial in contrast to the static case for which various series methods exist. In particular, the BBGKY approach developed for a classical gas is not directly transferable to a lattice gas because the equation for one-particle distribution function involves not only two-particle but also higher order distribution functions. Yet the analysis of the snapshots shows that aside from the critical point the system can be viewed as a gas of weekly interacting structural defects complicated by the presence of transient configurations.
Developing accurate analytical methods for disordered systems: Efficient perturbation expansion for disordered systems
It is an old idea that the perturbation series for the resolvent of a matrix can be rearranged so as to exclude the multiple scattering.
- In our work reported at Conference on Applied Physics (Kyiv, Ukraine, 2007) [pdf in ukrainian] we study this technique in detail. We observe that the believed improvement in convergence of the rearranged series is generally not valid, but is valid for sparse matrices, though the complications introduced by the rearrangement make its brute-force use inefficient. Nevertheless the constructive use of the method is possible: for matrices with i.i.d. random variables on their diagonal the rearrangement enables to take the average explicitly (note that some off-diagonal disorder, e.g. random bond model, can be reformulated as diagonal one).