Inorganic semiconductors

Semiconductors are materials with a bandgap and variable electronic conductivity used as the core component of optoelectronic devices. Several classes of semiconductors are distinguished by nature of participating electrons, see these slides.

• Emerging 2D semiconductors
• Mechanisms of light- and current-induced phenomena in pnictide and chalcogenide semiconductors
• Optical properties of nanostructured silicon
• Inverse problem for the luminescence

Emerging 2D semiconductors

Several electronically different classes of two-dimensional (2D) semiconductors are well known nowadays including graphene family, transition metal dichalcogenides, and pnictogens. Many of their unique properties remain poorely understood calling for in-depth theoretical study.

• Small Polarons in Two-Dimensional Pnictogens: A First-Principles Study, J Phys Chem Lett 12, 4674 (2021) [reprint]: In majority of crystalline multidimensional covalent semiconductors electrons and holes move as free quasiparticles because of large width of electronic bands compared to scattering strength. Pnictogens have a narrow subband of lone pair orbitals near the top of their valence band which can host hole polarons, and it turns out that such polarons are stable in the blue-allotrope of 2D pnictogens.

Mechanisms of light- and current-induced phenomena in pnictide and chalcogenide semiconductors

Amorphous pnictide and chalcogenide semiconductors (As, Se, As2Se3, Ge2Sb2Te5 etc., see the diagram and Library) exhibit significant photo- and current-induced changes whose nature is not well understood thus limiting the potential applications of the phenomenon (see for example phase-change memory).

• Electronic structure and the glass transition in pnictide and chalcogenide semiconductor alloys. I. The formation of the ppσ-network, J Chem Phys 133, 234503 (2010) [pdf, arXiv]: Many properties of pnictides and chalcogenides can be rationalized using the concept of ppσ-network of covalent and secondary bonds. The secondary bonding is significant in these electron-rich semiconductors and results in strong redistribution of electronic density diminishing the difference between front and back bonds.

• Electronic structure and the glass transition in pnictide and chalcogenide semiconductor alloys. II. The intrinsic electronic midgap states, J Chem Phys 133, 234504 (2010) [pdf, arXiv, presentation]: It is generally believed that light-induced changes are intimately related to midgap electronic states localized on coordination defects and their pairs. We show that strong secondary bonding in pnictides and chalcogenides results in the coordination defects linearly extended over several front and back bonds. Front-back bond switching makes the defects mobile which is the underlying mechanism of photo- and current-induced structural changes. Valence alternation pairs (VAP) of such coordination defects have very low energy, they are topologically stable and mobile via bond switching.

Optical properties of nanostructured silicon: Origin of anomalously slow decay of phosphorescence in porous silicon

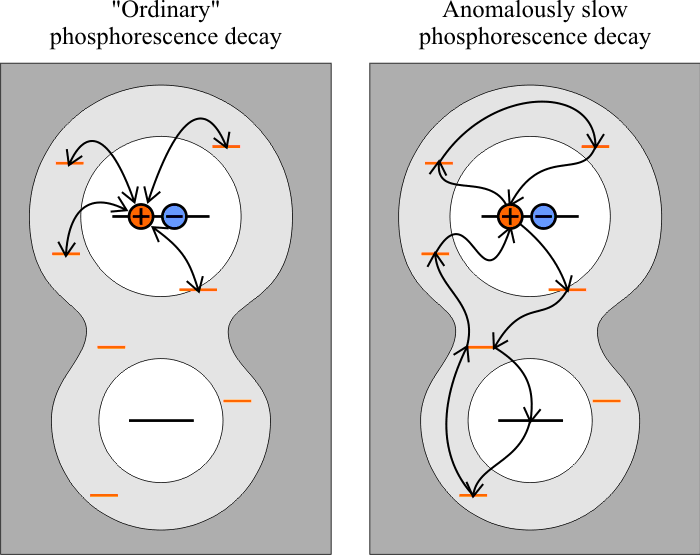
Nanostructured silicon (porous-Si, Si nanocrystals in SiO2, Si nanowires etc., see the Library) raised a wave of scientific activity in 1990 as the promising material for silicon based optoelectronics. The kinetics of the phosphorescence decay of a porous silicon in a wide temperature range is anomalously slow (the integral over the extrapolated signal diverges). This phenomena is observed in some conjugated polymers, but the existing explanation as the tunneling recombination of geminate electron-hole pairs requires an unnatural distribution of activation energies for porous silicon: wide, flat, with depression at small energies.

• New mechanism of charge carriers localization in silicon nanowires, Physics of Low-Dimensional Structures, n. 7/8, 25 (2003): We demonstrate that this is a generic feature of disordered systems with significant initial separation of the recombining particles: it is their multiple retrapping which is responsible for the depression of the distribution of activation energies. The comprehensive theory is published in PhD thesis.

Inverse problem for the luminescence

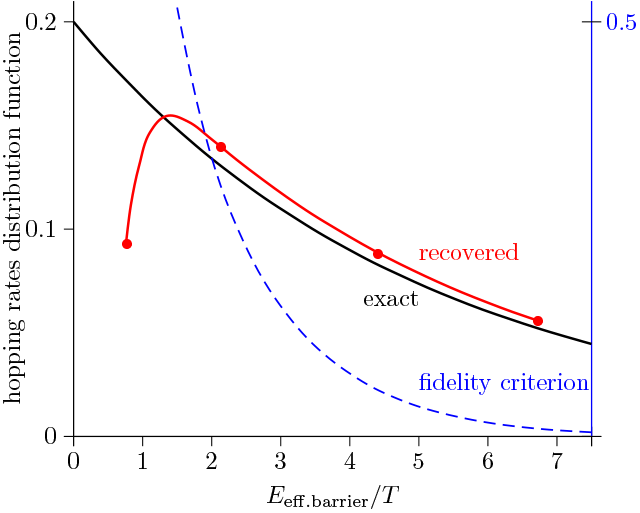
The analysis of the luminescence response is one of the easiest tools for studying the physical properties of materials. In particular, much information can be obtained by deconvoluting the time curve of the luminescence decay. The deconvolution is nontrivial, except the case of the multi-exponential decay, since the numerical inverse-Laplace transformation is mathematically incorrect problem.

• Influence of structural inhomogeneity on the luminescence properties of silicon nanocrystallites, Low Temperature Physics 28, 706 (2002) [pdf]: We derive robust inversion formulas for the power-law decay (see demonstration), observed for example in some conjugated polymers and nanostructured silicon as an after-glow or phosphorescence. This method applied for porous silicon is consistent with the measurements of the thermally stimulated luminescence complementing the latter at small activation energies. The comprehensive theory is published in PhD thesis.